A student is restricted to a monthly budget constraint of £200 which is allocated to two activities: 1 answer below » A student is restricted to a monthly budget constraint of £200 which is allocated to two activities: bridge and skating. His utility function is given by the equation U = 5x0.2y0.8, where x and y represent the number of hours spent on skating and bridge, respectively. Skating costs £5 per hour, while bridge costs £2 per hour. (a) Derive expressions for MUx and MUy. 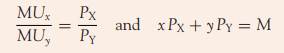(b) Solve the simultaneous equations (c) Use Lagrange multipliers to determine the number of hours that should be spent on each activity to maximise utility. Comment on the answers in (b) and (c).

 

A student is restricted to a monthly budget constraint of £200 which is allocated to two activities:1 answer below »

A student is restricted to a monthly budget constraint of £200 which is allocated to two activities: bridge and skating. His utility function is given by the equation U = 5x0.2y0.8, where x and y represent the number of hours spent on skating and bridge, respectively. Skating costs £5 per hour, while bridge costs £2 per hour.

(a) Derive expressions for MUx and MUy.

(b) Solve the simultaneous equations

(c) Use Lagrange multipliers to determine the number of hours that should be spent on each activity to maximise utility.

Comment on the answers in (b) and (c).

1 Approved Answer

Suhail M answered on January 20, 2022

5 Ratings,(9 Votes)

) Utility function U = 5 * x^0.2 * y^0.8 ------------------(1) Ux =  მსმ: = (y / x) ^ 0.8 Uy = helne = 4 * (x/y)^0.2 Again, monthly budget constraint (M) = (5 x + 2 y) < = 200 \varepsilon -------------(2) Assuming x hrs & y hrs respectively spent on skating & bridge So, M Ux = (5x + 2y) * (y/x)^0.8 <= 200 * (y/x)^0.8 & M Uy = 4 (5x + 2y) * (x/y)^0.2 <= 200*(x/y)^0.2 b) Based on Langranges' multiplier lambda, we can combine equation (1) & (2) for obtaining maxima / minima as: gradient (5 * x^0.2 * y^0.8) =  lambda * gradient (5x + 2y - 200) Ux i + Uy j = lambda * (5 i + 2 j) (ymax / xmax) ^ 0.8 = 5 * lambda --------------(3) 2 * (xmax / ymax)^0.2 = lambda ---------------(4) Solving, for lambda, we have, lambda = (16/5)^0.2 So, 2^5 * xmax / ymax = 16/5 \Rightarrow   xmax / ymax = 1/10 \Rightarrow ymax = 10 xmax Putting this in the budget constraint equation (2), we have, 5 xmax + 2 * 10 xmax - 200 = 0 xmax = 8 & ymax = 80 For xmax = 8 hours on skating & ymax = 10 hrs on bridge, utility function is maximized c) Maximum utility level achieved = 5 * xmax ^ 0.2 * ymax ^ 0.8 = 5 * 8 ^ 0.2 * 80 ^ 0.8 = 252.38 e) The student planning to spend 8 hours on skating & 10 hours on bridge, can achieve a maximum utility value of around 252, withiout exceeding his budget cost constraint of 200 \varepsilon.